Problem Solving/백준
[백준/C++] 6549번 히스토그램 분할정복 증명
높은곳에영광
2022. 11. 28. 21:57
일단 그리디 하게 풀어서는 문제의 정답을 구할 수 없고, dp로 풀기에는 배열의 크기가 압도적으로 모자란 것으로 확인했다.
모든 배열 10만개를 훑기에는 n2부터는 time complexity에 문제가 생길 것 같았다.
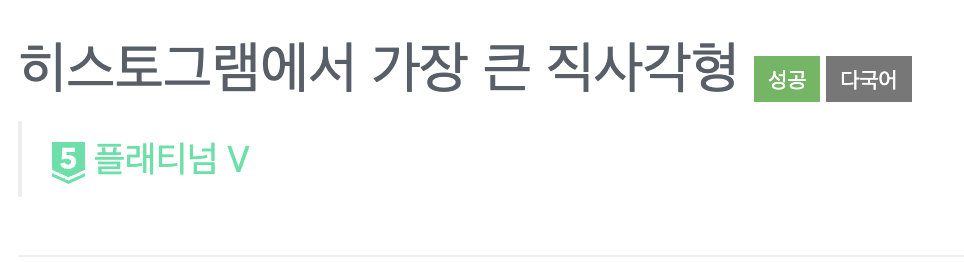
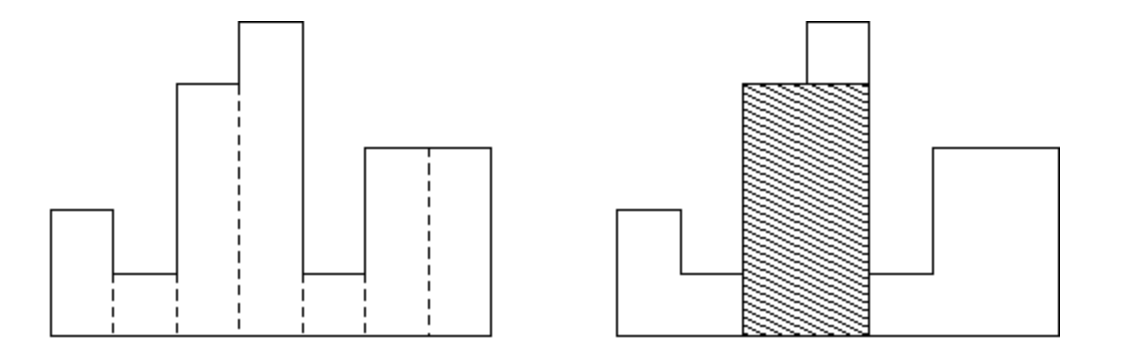
그래서 분할 정복으로 왼쪽 오른쪽 나눠서 진행하면 어떨까? 하는 생각을 하게 되었지만, 각각 방향에서 최댓값은 찾을 수 있으나 다른 방향을 걸쳐서(가운데 부분에서) 최댓값을 구하는 경우면 어떻게 하나 고민하게 되었다.
고민 결과 아래와 같은 이유로 가운데가 포함된 경우 그리디 하게 모든 직사각형을 가져가는 것이 맞다고 생각하게 되었다.
Prove
- 가운데가 포함된 직사각형에서 더 큰 방향의 막대를 포함하여 크기를 계산하면 최댓값을 구할 수 있다.
Basis
- 가운데 막대가 포함된 경우에서 최댓값이 있다고 가정한다.
- 가운데를 제외한 왼쪽 부분의 최댓값, 오른쪽 부분의 최댓값은 분할 정복으로 구했다고 가정한다.
Assume
가운데에서 최댓값이 나오는 경우는 아래 두 가지 경우와 같다.
- 가운데가 포함되려면 왼쪽 부분합이나 오른쪽 부분합의 최댓값이 중앙 막대와 맞닿은 최댓값이거나
- 왼쪽이나 오른쪽 부분합에서 중앙값을 추가했을 때 최댓값인지 고려할 것이니 중앙값이 포함된다.
- 현재 진행 방향으로 막대를 확장할 경우(진행 방향 막대가 반대 방향 막대보다 큰 경우) 최댓값을 구할 수 있다.
- 반대 반향으로 진행할 때에도 반대 막대가 더 큰 경우이므로 포함시키고 계산하여 최댓값을 구할 수 있다.
- 가운데에서 양 옆으로 늘어나는 형태일 것이다.
- 가운데에서 옆으로 늘어나기 위해서 큰 것을 먼저 취하며 진행하며 모든 막대를 훑으므로 최댓값을 구할 수 있다.
#include <bits/stdc++.h>
#define ll long long
using namespace std ;
vector<int> hist ;
int N ;
//find mid range maximum value
ll int find_mid_max(int sp, int mid, int ep)
{
int height = hist[mid] ;
int lhs = mid - 1 ;
int rhs = mid + 1 ;
int width = 1 ;
ll int local_max = width * height ;
while(lhs >= sp || rhs <= ep)
{
if(lhs < sp)
height = min(height, hist[rhs++]) ;
else if(rhs > ep)
height = min(height, hist[lhs--]) ;
else if(hist[lhs] > hist[rhs])
height = min(height, hist[lhs--]) ;
else
height = min(height, hist[rhs++]) ;
local_max = max(local_max, (ll int)(++width) * height) ;
}
return local_max ;
}
//find divide and conquer
ll int find_div_and_con(int sp, int ep)
{
if(sp == ep) return hist[sp] ;
//만약 왼쪽 끝자락이 포함되지 않는다면 rhs에서 정답을 찾았을 것이고
//포함된다면 최대한 greedy하게 포함하면서 모든 사각형을 훑어보면 될 것이다.
int mid = (sp + ep) / 2 ;
ll int mid_max = find_mid_max(sp, mid, ep) ;
ll int lr_max = max(find_div_and_con(sp, mid), find_div_and_con(mid + 1, ep));
return max(mid_max, lr_max) ;
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0) ;
while(1)
{
cin >> N ;
if(N == 0) break ;
hist.clear() ;
hist.resize(N) ;
for(int &it : hist)
cin >> it ;
cout << find_div_and_con(0, N - 1) << "\n" ;
}
}느낀 점: 분할 정복을 아직 정복하지 못했다.... 가운데 부분 계산 생각만 3일 정도 한 것 같은데 더 꾸준히 공부해야겠다.
추가로 MAX를 define 해서 3가지를 동시에 비교하게 하는 것과 max stl을 2번 사용하는 것에 속도 차이가 있다는 것을 알게 되었다.
문제: https://www.acmicpc.net/problem/6549
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net